System stawkowania Kelly jest znany jako ten, który daje najbardziej optymalne tempo wzrostu zysków. Niestety jest on jednocześnie szalenie niestabilny, a sam wynalazca systemu – John Larry Kelly Junior – nie stosował go w praktyce. System ten jest polecany osobom, które są gotowe zaryzykować całość kapitału, aby w relatywnie krótkim czasie szybko się wzbogacić. Stosowanie tego systemu w dłuższym okresie czasu nie spełnia podstawowego warunku koniecznego, czyli ochrony kapitału. Na pewno warto poznać jego założenia i najpopularniejsze modyfikacje, bo jeśli masz dużą przewagę nad bukmacherem albo trafia Ci się jednorazowa okazja, to może być on bardzo pomocny.

Amerykanin John Larry Kelly Junior – autor kryterium Kelly’ego
Spis treści
1. Kim jest John Kelly?
Kryterium Kelly (ang. Kelly criterion) jest wzorem na matematycznie optymalne zarządzanie pieniędzmi. Pasjonuje graczy zakładów sportowych, karciarzy, inwestorów, managerów i ekonomistów.
Formuła Kelly’ego została po raz pierwszy opisana w 1956 roku przez naukowca John’a Kelly’ego (1923 – 1965).
John Larry Kelly, Jr. urodził się w stanie Texas w USA. Spędził 4 lata w USA Navy jako pilot podczas II Wojny Światowej. W 1953 uzyskał tytuł doktora w dziedzinie fizyki.
W 1962 roku Kelly użył komputera do syntezy mowy, która została użyta w jednym z ówczesnych filmów.
Kelly zmarł na udar mózgu na chodniku Manhattanu w młodym wieku 41 lat. Mówi się, że nigdy nie używał własnego kryterium, aby zarabiać pieniądze.
Polecany bukmacher:

2. Wprowadzenie
Kryterium Kelly jest wzorem używanym do maksymalizowania długoterminowego współczynnika tempa wzrostu powtarzalnych gier o podanym ryzyku, które mają pozytywną wartość oczekiwaną. Formuła Kelly’ego określa jaki procent bieżącego bankrolla należy postawić na każdym etapie gry.
System Kelly maksymalizuje współczynnik tempa wzrostu w długim okresie, a zatem także minimalizuje ryzyko ruiny, ale to ryzyko jest różne od zera. Używając systemu Kelly nie możemy doprowadzić do bankructwa, ale wartość bankrolla może zmierzać do 0 jednostek. A zatem skończone prawdopodobieństwo ruiny istnieje. Założeniem wzoru jest nieskończona podzielność stawek, co nie powinno przeszkadzać w praktyce, jeśli bankroll jest wystarczająco duży.
3. Obliczenia
Tw. (Kryterium Kelly’ego)
Długoterminowy współczynnik wzrostu jest maksymalizowany przez znalezienie ułamka f* z bankrollu, który maksymalizuje wartość oczekiwaną logarytmu rezultatów[1]. Dla zakładów z dwoma wynikami, gdzie jeden powoduje utratę całych środków na zakład, a drugi zawiera zwycięską kwotę pomnożoną przez oferowany kurs, ułamek f* obliczamy za pomocą wzoru:
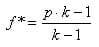
gdzie:
- f* jest ułamkiem przeznaczonego na grę kapitału do postawienia;
- k jest kursem oferowanym na zakład;
- p jest prawdopodobieństwem wygranej (p = 1-q).
Przykład
Poniższe przykłady są liczone dla pk=1,10 (yield=10%) i pk=1,05 (yield=5%), ponieważ dobrzy typerzy osiągają długoterminowy yield min. 5%.
Przykłady te mają na celu zobrazować zależność f* od wielkości ilorazu prawdopodobieństwa/kursu. Dla innych wartości pk>1 zależności te będą podobne.
yield = 10%
p = 99%, k = 1,11 → f* = 9,9%
p = 90%, k = 1,22 → f* = 4,95%
p = 75% , k = 1,47 → f* = 2,36%
p = 50%, k = 2,20 → f* = 0,92%
p = 25%, k = 4,40 → f* = 0,32%
p = 10%, k = 11,0 → f* = 0,11%
yield = 5%
p = 99%, k = 1,06 → f* = 17,33%
p = 90%, k = 1,17 → f* = 6,3%
p = 75% , k = 1,40 → f* = 2,63%
p = 50%, k = 2,10 → f* = 0,95%
p = 25%, k = 4,20 → f* = 0,33%
p = 10%, k = 10,5 → f* = 0,11%
Z podanego przykładu można wysnuć następujące wnioski:
- Im większy yield gracza, tym mniejszą kwotę kapitału musi on ryzykować.
- Im większy kurs, tym mniejsza stawka jaką należy postawić.
- Dla kursów mniejszych od 1,40 wartość stawki jaką powinien postawić gracz jest niebezpiecznie wysoka i mimo iż zapewnia optymalny wzrost posiadanego kapitału, stwarza realne zagrożenie dla budżetu gracza.
FAKT 1:
Zawodowi gracze rzadko grają kursy mniejsze od 1,40 chyba że mają one duże value.
FAKT 2:
Zawodowi gracze przy stawkowaniu stosują zasadę odwrotnej proporcjonalności, czyli stawiają mniej na wysokie kursy, a więcej na niższe kursy.
Dowód twierdzenia Kelly’ego
Załóżmy, że szukamy ułamka f (0 < f < 1) obecnego bankrollu B, a oferowany kurs wynosi k (w oryginalnym źródle angielskim v=k-1). Jeśli wygramy otrzymamy zysk v·f·B; w przypadku zaś porażki tracimy f·B i nowy bankroll ma postać:
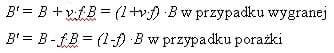
Przyjmijmy, że gramy wielokrotnie przyjmując “nowy” bankroll (oznaczony B’) po grze jako “stary” bankroll (oznaczony B) dla kolejnej gry. Zakładamy, że gra i kursy się nie zmieniają i nie zmieniamy naszej strategii podczas gry (stawiania ułamka z bankrollu).
Przypuśćmy, że wygraliśmy w razy z n wszystkich gier i przegraliśmy n-w razy. Aby znaleźć nowy bankroll, potrzebujemy pomnożyć przez [1+(k-1)·f] początkowy bankroll w razy (“współczynnik wygranych”) oraz przez (‘, 1-f) pomnożyć (n-w) razy (“współczynnik przegranych”):
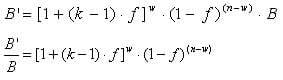
To dało nam współczynnik zmiany bankrollu od początku, czyli po n grach. Oznaczmy przez y średni współczynnik zmiany bankrolla na grę. Wtedy po n grach, bankroll wzrośnie o czynnik y^n:
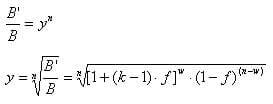
Wartość f dla której funkcja y(f) osiąga maksimum jest taka sama jak dla funkcji ln [y(f)] (wynika z monotoniczności i różnowartościowości funkcji ln):
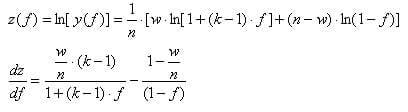
Przyjmując p=w/n, q=1-p i przyrównując prawą stronę do zera, otrzymujemy:
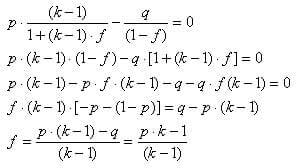
Ponieważ przy n dążącym do nieskończoności w/n zmierza do p oraz 1-w/n zmierza do q, dlatego powyższa równość jest optymalnym współczynnikiem maksymalizującym zyski w długim okresie czasu przy podanych założeniach i f*=f co należało dowieźć.
Idea systemu Kelly jest oparta na podejmowaniu gry o ustalonym kursie i prawdopodobieństwie. W dowodzie jest wykorzystane założenie, że granica lim(liczba wygranych)/(liczba gier) dąży do określonego prawdopodobieństwa. W zakładach bukmacherskich nie mamy do czynienia ze stałymi p i k, lecz z serią zakładów o różnych p i k za każdym razem. Gdyby jednak dostosować model i do tego założenia, rezultat byłby identyczny – wzór miałby zastosowanie do każdej pojedynczej próby.
4. Ułamkowy system Kelly
Nie zawsze musimy stawiać wartość f*, którą podaje nam system[2].
Niech B będzie początkową wartością bankrolla (BR). Wtedy jeśli stawiamy pełen system 100% Kelly (f=1), mamy następujący wzór na prawdopodobieństwo osiągnięcia kapitału wartości y·B zanim spadnie do x·B:
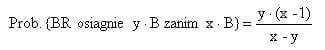
Ogólnie dla dowolnego f (ułamkowy system Kelly)

Przykład
Gracz ma 40% szanse wygrania (p = 0.40, q = 0.60), a oferowany kurs na zdarzenie wynosi k=3,00. Używając systemu Kelly powinien on postawić 10% bankrolla na każdą możliwość (f*=0.10), aby zmaksymalizować długoterminowy współczynnik wzrostu bankrolla.
Jeśli value=1 lub mniejsze od 1, np. jeśli k ≤ q/p+1, wtedy gracz nie powinien stawiać.
Reguła upraszcza się dla k = 2,00 do postaci:
f* = p-q = 2•p-1
i można ją sformułować słowami:
Stawiaj taki ułamek bankrolla, który jest równy twojej procentowej przewadze.
5. Wady i zalety systemu Kelly
Używanie systemu Kelly w praktyce ma również swoje wady. Kiedy są robione serie zakładów, szansa spadku do 1/n bankrolla wynosi 1/n. Zatem mamy 50% szanse w pewnym momencie stracenia 50% bankrolla, 10% szanse utraty do poziomu 10% itd.
Optymalny współczynnik wzrostu bankrolla zapewnia stawianie pełnych stawek sugerowanych przez kryterium Kelly‘ego (f=1), ale to powoduje niestabilne wyniki. Są szanse 1/3 na uzyskanie połowy bankrolla zanim się go podwoi, co uzyskujemy korzystając ze wzoru wyżej dla y = 2; x = 1 otrzymujemy 2/3.
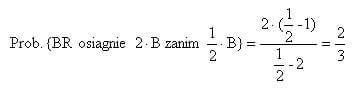
Popularną alternatywą jest stawianie połowy sugerowanej kwoty (f = ½ ), co daje 3/4 zwrotu z zainwestowanego kapitału z o wiele mniejszą niestabilnością. Przy zastosowaniu systemu Kelly‘ego generującego procent złożony wzrostu 9,06% z pełnymi stawkami, połowiczne stawki mogą zgromadzić procentowy współczynnik wzrostu 7,5%.
Nadstawkowanie ponad sugestie systemu zmniejsza wydajność, jako że długofalowy współczynnik wzrostu spada do zera, kiedy stawki Kelly’ego zmierzają do podwojenia. Używanie zakładów ½-Kelly także zabezpiecza przeciw zrujnowaniu przez nadstawkowanie.
Powyższy system stosuje się do serii zakładów. Lepiej jest je dywersyfikować. Przykładowo gracz, który stawia na każdego konia w biegu używając kryterium Kelly zrobi lepszy średni długofalowy zwrot niż gracz, który stawia tylko na jednego konia w biegu. Podobnie w zakładach bukmacherskich i na rynku papierów wartościowych[3].
Z działu Arkusze Excel możesz pobrać arkusz kalkulacyjny pomocny w stosowaniu systemu Kelly.
6. Zastosowanie Kelly w hazardzie
O ile system Kelly jest wzorem na optymalne dobieranie stawek pod kątem maksymalizacji zysku, o tyle nie uwzględnia on w ogóle dbałości o stabilność kapitału (brak znaczących wahań). System warto rozważyć przy małym kapitale na grze, w przypadku gdy gracz zamierza go szybko pomnożyć w możliwie optymalny sposób, kosztem dużego ryzyka utraty znacznej części kapitału.
System może mieć zastosowanie w turniejach pokerowych jako strategia stawkowania w początkowej fazie budowania bankrolla. Potem można zmienić stawkowanie na ułamkowy Kelly lub na inny “bezpieczny” system.
Tam gdzie kasyno ma przewagę nad graczami, systemu Kelly’ego nie stosuje się.
Choć model Kelly nie ma zastosowania w zakładach bukmacherskich przy dużym kapitale, to wyjaśnia dlaczego nie warto stawiać niskich kursów i stosować zasadę odwróconej proporcjonalności.
Literatura
[1] A bet you can’t refuse – źródło obliczeń z grupy dyskusyjnej
[2] Two Risk of Ruin Equations – równania dot. ułamkowego systemu Kelly
[3] Ile można zaryzykować w jednej transakcji – artykuł o wykorzystywaniu systemu Kelly na Giełdzie Papierów Wartościowych
Zobacz też:
Porównanie systemów bukmacherskich
stawkowanie 1-10j
Polecany bukmacher:

Jak możemy poprawić artykuł?
Jeśli chciałbyś dać nam możliwość odpowiedzi, to podaj email:
Dziękujemy za przesłanie opinii.




