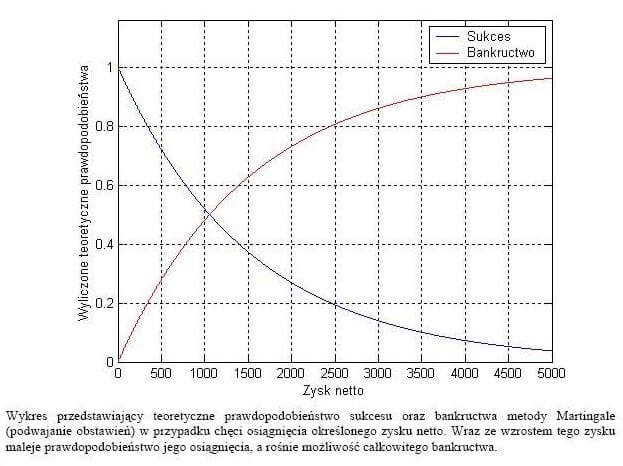
Martingale jest najstarszą i najbardziej znaną progresją na “podwajanie stawki”. Pewnie dlatego nazywa się ją progresją klasyczną. Wielu naciągaczy zachwala ten system jako idealną metodę na ogranie kasyna. Prawda jest taka, że prowadzi do bankructwa, bo nikt nie dysponuje nieskończonym kapitałem…

System Martingale jest systemem podwajania stawki po każdej przegranej i powrotu do stawki początkowej po wygranej.
Spis treści
1. Idea Martingale
System Martingale (a dokładniej rodzaj stawkowania typu Martingale) polega na podwajaniu stawek po przegranej i powrotu do pierwotnej stawki po wygranej (przy założeniu, że wygrana jest dwukrotnością stawki).
W ten sposób wszystkie straty zostają odrobione z zyskiem, który jest równy początkowej stawce, a “cykl do pierwszej wygranej” zaczyna się od nowa, np.:
| Rzut | Stawka | Wynik | Saldo |
|---|---|---|---|
| 1 | 1 | Przegrana | -1 |
| 2 | 2 | Przegrana | -3 |
| 3 | 4 | Wygrana | +1 |
| 4 | 1 | Przegrana | 0 |
| 5 | 2 | Przegrana | -2 |
| 6 | 4 | Przegrana | -6 |
| 7 | 8 | Wygrana | +2 |
Na pierwszy rzut oka nic nie budzi podejrzeń. Gracz z całą pewnością kiedyś wygra i dlatego strategia stawkowania Martingale była widziana jako gwarancja sukcesu przez tych, którzy ją praktykowali. W długiej perspektywie stawki rosną w postępie geometrycznym i w końcu musi nastąpić czarna seria, która zgromadzi 20 albo nawet 30 porażek pod rząd (serie 10-20 porażek z rzędu na czarne/czerwone nie są niczym nadzwyczajnym w ruletce). To powoduje ruinę gracza.
Owszem, gracz zawsze wygra +1 jednostkę w cyklu, ale musi spełnić 2 warunki:
- Musi mieć pieniądze na kolejną stawkę.
- Operator hazardowy musi chcieć przyjąć od niego tą stawkę.
Pierwszy punkt sprowadza się do tego, że gracz musi być nieskończenie bogaty. Nie ma takich ludzi, więc to oznacza, że bankructwo takiego gracza jest kwestią czasu.
Drugi punkt jest często barierą po stronie bukmachera/kasyna, który nie chce zbyt długo czekać na porażkę gracza i woli zrealizować “mniejszy zysk” ograniczając stawkę graczy i własne ryzyko. Ponieważ limity stawek zredukowały ryzyko kasyna, sam system Martingale NIE stanowi już zagrożenia dla żadnego kasyna.
Polecany bukmacher:

2. Historia Martingale
Pierwotnie Martingale było strategią zakładów popularną w XVIII–wiecznej Francji. Strategia ta polegała na podwajaniu stawki w przypadku przegranej i była stosowana głównie do ruletek.
Plotka głosi, że twórcą systemu jest John Henry Martindale, którego nazwisko zostało z biegiem czasu przekręcone na Martingale. Podobno zachęcał graczy do używania go w swoim londyńskim kasynie. Był tak przekonany, że kasyno zawsze wygra, że nakłaniał graczy do podwajania stawek aż do momentu, gdy jedno z jego kasyn zaczęło mieć problemy.
W roku 1891 strategii Martingale użył z sukcesem w ruletce legendarny Charles Wells (1841-1922), który rozbił bank kasyna w Monte Carlo 12 razy w ciągu 3 dni! Stał się tym samym inspiracją do piosenki “Facet który rozbił bank w Monte Carlo“[1].
3. Obliczenia Martingale
Niech q będzie prawdopodobieństwem porażki (np. dla ruletki amerykańskiej q=20/38).
Niech y będzie kwotą rozpoczynającą zakład (np. $10).
Niech x będzie skończoną liczbą zakładów, na które gracz może sobie pozwolić przegrać (długość możliwej “czarnej serii”).
Prawdopodobieństwo, że gracz przegra wszystkie x zakładów wynosi q^x.
Wtedy gracz traci kwotę:
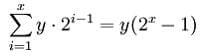
Prawdopodobieństwo nie przegrania wszystkich x zakładów wynosi 1 – q^x.
Wtedy gracz wygrywa kwotę pieniędzy y.
Wartość oczekiwana zysku na etap wynosi:
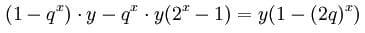
Jeśli q > ¼ , wyrażenie 1 – (2q)^x < 0 dla każdego x > 0.
To oznacza, że dla każdej gry, gdzie jest bardziej możliwe przegrać niż wygrać, gracz będzie średnio przegrywał pieniądze.
Ponadto im więcej razy będzie się zakładał, tym więcej straci.
4. Przykład 1

Ruletka amerykańska,
fot. Shutterstock
Załóżmy, że gracz stosuje system Martingale do amerykańskiej ruletki (z dodatkowymi polami 0 i 00) na czerwone lub czarne kolory, które wygrywają średnio 18 razy z 38[2]. Jeśli początkowy kapitał gracza (bankroll) wynosi $150, a początkowy zakład $10, to gracz może pozwolić sobie na 4 zakłady z rzędu ($10, $20, $40 i $80) zanim straci pieniądze. Jeśli któryś z tych 4 zakładów wygra, odrabia straty i zyskuje dodatkowo $10.
Szansa 4 porażek pod rząd (a zatem utraty całych $150) wynosi (20/38)^4 = 7,67%. Pozostałe 92,3% to szansa wygrania $10.
Grę do przegranej 4 razy z rzędu albo do wygranej nazwiemy jednym etapem.
Powtarzając etapy, średni zysk wyniesie (0.923·$10) – (0.0767·$150) = -$2.275 na etap.
Zatem gracz traci średnio $2.275 w każdym etapie.
Jednakże jeśli gracz posiada nieskończoną kwotę pieniędzy, oczekiwany zwrot wynosi (18/38)·s na rundę (gdzie s jest początkową stawką).
Z początkowym zakładem $10, oczekiwany zwrot wynosi $4.736 na etap.
5. Przykład 2
Kliknij poniższy obrazek, aby zobaczyć pełną treść zadania.
Zgodnie z powyższym wykresem widać, że szansa na podwojenie kwoty to ok. 30% (czyli zdobycie kwoty 2047zł dla tego przykładu).
Pozostałe ok. 70% to prawdopodobieństwo bankructwa.
6. Symulacja Martingale
Poniżej przedstawione są 4 wykresy ilustrujące wartość kapitału gracza w zależności od ilości postawionych zakładów, zaczynając od krótkich serii 100 zakładów do długich z 1 mln zakładami[3]. Te wykresy bardzo dobrze pokazują różnice pomiędzy małą a dużą próbą. Wszystkie zakłady są z kursem dziesiętnym k=2.0 dla uproszczenia i szansą sukcesu ok. 50%.
Pierwszy wykres pokazuje wszystkie wygrane i straty dla gracza Martingale grającego 100 zakładów.
Na początku widzimy maleńki wzrost ledwo widoczny na wykresie, po czym duży spadek do straty -500 jednostek, spowodowany długim łańcuchem porażek, gdzie zakłady były podwajane. W końcu wygrana przywróciła nas do wcześniejszego wysokiego punktu +1 jednostka.
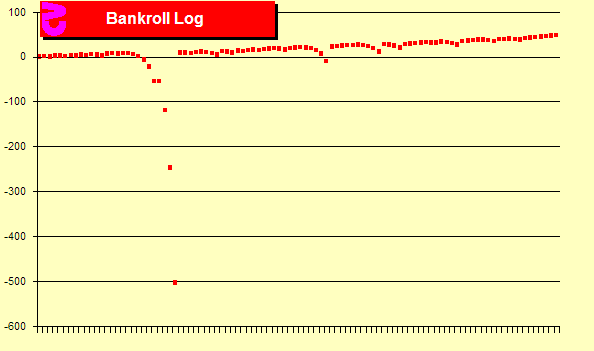
Wykres kapitału w próbie 100 zakładów, Źródło: BlackJackInColor.com
Kolejny wykres jest dla 1.000 zakładów w grupach po 10.
Widzimy na nim 500 jednostkowy spadek. Po nim dosyć szczęśliwa passa bez poważnej straty przez około 8.000 zakładów.
W końcu znów widzimy duży spadek, ale tym razem aż do –1.700 jednostek, zanim udało się wygrać +1 jednostkę na czysto.
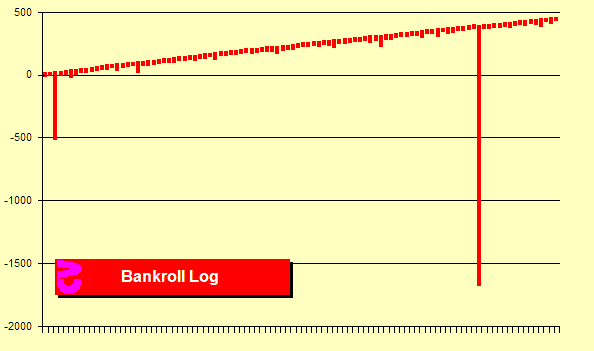
Wykres kapitału w próbie 1000 zakładów, Źródło: BlackJackInColor.com
Kontynuujmy rozważania do 100.000 zakładów w grupach po 1.000.
Widzimy, że oś y poszerzyła zakres od –40.000 jednostek do +50.000 jednostek.
Linia zaczyna wyglądać bardziej płynnie, ale możemy zauważyć poważne obsunięcia.
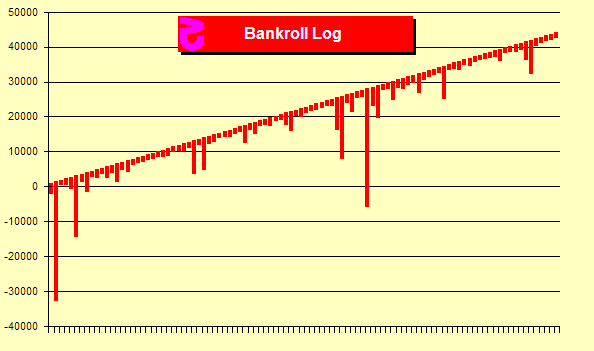
Wykres kapitału w próbie 100.000 zakładów, Źródło: BlackJackInColor.com
Wreszcie 1.000.000 zakładów w grupach po 10.000.
Zaczęliśmy tutaj z zerowym zyskiem, a zakończyliśmy z prawie +500.000 jednostek zysku. Jednakże pojawiła się jedna strata (wywołana łańcuchem 22 porażek z rzędu = 21,2 w ruletce francuskiej = 20,4 w ruletce amerykańskiej), wymagająca zakładu 4.000.000 jednostek (dla początkowej stawki 1$ będzie to stawka 4 mln USD), by odzyskać stawkę i uzyskać wygraną +1 jednostka.
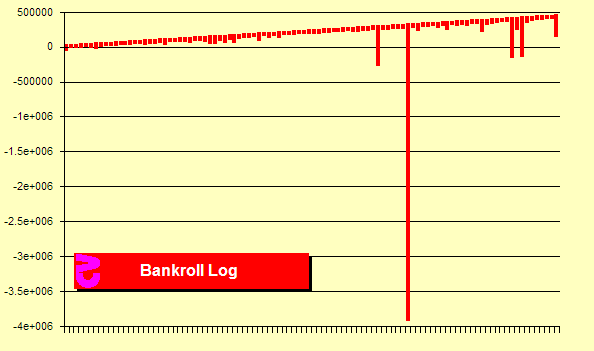
Wykres kapitału w próbie 1.000.000 zakładów, Źródło: BlackJackInColor.com
Oczywiście to tylko przykładowe symulacje. W rzeczywistości spadki będą miały różne wielkości w różnym czasie. Porównałbym to do “gry w krzesła z przerywaną muzyką” albo do podawania granatu z ręki do ręki.
7. Płaska stawka czy Martingale?
Płaska stawka (taka sama stawka na każdy zakład) powinna być domyślnym systemem każdego gracza. Jeśli wyższość innego systemu stawkowania nie została udowodniona w testach, to gracz powinien pozostać przy płaskiej stawce, aby zminimalizować wahania kapitału i ryzyko bankructwa.
Duże wahania kapitału mają duży negatywny wpływ na psychikę gracza, a wiadomo, że pod wpływem emocji nie działa się racjonalnie, co bywa bardzo kosztowne i jest wykorzystywane w kasynach.
Przyjrzyjmy się zatem na koniec jeszcze jednemu wykresowi.
Porównuje on dwa systemy stawkowania:
- płaską stawkę
- Martingale
Poniższy wykres pokazuje rozkład prawdopodobieństwa końcowego kapitału dla planu z wartością oczekiwaną 150 jednostek.
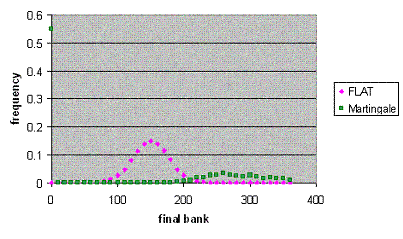
Porównanie płaskiej stawki z Martingale
Przy płaskiej stawce (kolor różowy) gracz może się spodziewać, że jego kapitał będzie po serii zakładów najprawdopodobniej w przedziale od 80 do 220 jednostek.
Dla stawkowania Martingale widać, że kapitał będzie prawdopodobnie gdzieś w przedziale powyżej 180 jednostek.
Na pierwszy rzut oka wydaje się zatem, że system Martingale ma znaczną przewagę nad płaską stawką (z uwagi na wyraźnie większy kapitał możliwy do uzyskania). Upewnij się jednak, że nie przeoczyłeś małej zielonej kropeczki w lewym górnym rogu wykresu, która mówi o tym, że prawdopodobieństwo bankructwa dla stawkowania Martingale wynosi 55%! (0% dla płaskiej stawki)
8. Warianty Martingale
System Martingale jest stosowany w zakładach bukmacherskich zwykle do zakładów AKO z kursem ok. @2.0 (powinny mieć value>1).
Nic jednak nie stoi na przeszkodzie w posunięciu się o krok dalej i wyciągnięcie wniosków dla innych wartości AKO (im wyższy kurs, tym wyższe ryzyko bankructwa). Można też rozważać mniejsze kursy od @2.0.
9. Wnioski
Nie istnieje taki kapitał, który byłby wystarczająco duży, aby wytrzymać serię porażek.
Wraz ze wzrostem długości czarnej serii rośnie ryzyko utraty pieniędzy. Stawki mogą przekroczyć możliwości finansowe gracza. Pojawi się strach i niepewność. Być może poczucie bezsilności lub desperacja. Nie są to warunki sprzyjające racjonalnym decyzjom. Jeśli chcesz stosować Martingale, to zalecam z góry ustalić kapitał do przegrania oraz moment wyjścia.
Do oszacowania przydatności tego modelu stawkowania gracz powinien porównać prawdopodobieństwo podwojenia kapitału początkowego z prawdopodobieństwem bankructwa.
Długoterminowa przewaga gracza/kasyna jest pochodną prawdopodobieństwa sukcesu w pojedynczej próbie.
Jeśli value=p*k>1, to przewagę ma gracz, a jeśli value=p*k<1, to przewagę ma kasyno.
Jeśli kasyno ma długoterminową przewagę, to gracz powinien podejmować grę wtedy i tylko wtedy, gdy może on uzyskać krótkoterminową przewagę, np. dzięki bonusowi lub promocji.
10. Zakończenie
Jak widać powyżej system Martingale daje zysk tylko przy nieskończenie dużym kapitale na grę. W praktyce nikt takiego nie posiada, więc stosując go, jest kwestią czasu, gdy będziesz zmuszony obstawiać bardzo wysokie stawki.
Jak zareaguje na to Twoja psychika?
Kiedy “pękniesz”?
Zatrzymasz się przed wyznaczonym momentem?
A może przekroczysz wyznaczony budżet, aby tylko odrobić straty??
W dodatku możesz napotkać limit stawki ze strony bukmachera/kasyna, co ograniczy ilość możliwych etapów do zagrania.
Z ww. powodów Martingale nie jest systemem, który polecam. Gracz, który chce go używać powinien być świadomy ryzyka, jakie podejmuje i być odporny psychicznie. W pewnych przypadkach zalety systemu mogą niwelować wady.
System Martingale jest tożsamy z obstawianiem ogromnych pieniędzy po bardzo małym kursie. Przynosi więc bardzo małe, regularne zyski, aż nie trafi się na czarną serię. Jeśli będzie wystarczająco długa, to gracz straci mnóstwo pieniędzy.
Polecałbym pozostanie przy płaskiej stawce i trzymanie się zasad stopniowego budowania kapitału:
Literatura
[1] Casino Games Online – czeska strona sprzed 2009 roku
[2] Ruletka, Black Jack, zakłady bukmacherskie – hazard widziany oczami matematyka
[3] Martingale Long Term vs. Short Term – wykresy Martingale dla gry Black Jack
[4] The Truth about Betting Systems – Prawda o systemach bukmacherskich
Polecany bukmacher:

Przepraszamy.
Jak możemy poprawić artykuł?
Dziękujemy za przesłanie opinii.