Do określenia ryzyka w zakładach bukmacherskich potrzeba znać 3 rzeczy: kurs, prawdopodobieństwo sukcesu i wielkość stawki. Na tej podstawie możemy oszacować wielkość ryzyka, z którego wynika np. to, że stawianie kursu 2.0 za 100 PLN jest bardziej ryzykowne niż stawianie kursu 4.0 za 50 PLN.

14. Naturalne predyspozycje, Źródło: SureBety.pl
Spis treści
1. Definicja ryzyka

Ciężko przewidzieć wynik pojedynczego zdarzenia, ale wynik serii rzutów jest już łatwiejszy do przewidzenia, fot. ShutterStock
Duże ryzyko, ryzykowny skok, warty ryzyka, ryzyk fizyk, lubić ryzyko, unikać ryzyka, na własne ryzyko – skojarzenia z ryzykiem mamy różne.
Pojęcie ryzyka jest nieodłącznie związane ze zdarzeniami losowymi. Cytując Ralph’a Vince’a: Podrzuć do góry monetę. Przez chwilę będziesz doświadczał jednego z najbardziej fascynujących paradoksów natury – procesu przypadkowości. Kiedy moneta znajduje się w powietrzu, nie istnieje sposób na to, by z całą pewnością stwierdzić, na którą stronę ona spadnie, orła czy też reszki. Jednak po wielu rzutach wynik można racjonalnie przewidzieć.
2. Czym jest ryzyko?
Ryzyko zdaniem ekonomistów oznacza możliwość osiągnięcia wartości końcowej kapitału (inwestycji) różnej od wartości oczekiwanej.
przy czym wartość oczekiwaną gry liczymy ze wzoru:
EV (w1, w2, p1, p2) = p1⋅w1 + p2⋅w2 (równanie 1.1)
gdzie:
EV – wartość oczekiwana w grze z dwoma opcjami wypłat w1, w2; można uogólnić dla n czynników (ang. expected value)
w1, w2 – wartości wypłat,
p1, p2 – prawdopodobieństwo z którym wystąpi odpowiednia wypłata
Ciężko policzyć wartość oczekiwaną całej oferty bukmachera. Prawdopodobnie wyszłaby EV<0, czyli gra byłaby niekorzystna. Jednakże istnieją rynki na których EV>0 i celem gracza jest znalezienie tych rynków postawienie zakładów właśnie tam.
Dla potrzeb oszacowania opłacalności zakładu korzysta się w praktyce z parametru
Value = p⋅k = 1 + (EV dla stawki 1€) (równanie 1.2)
gdzie:
Value – wartość zakładu; jeśli większa od 1, to zakład z pozytywną wartością oczekiwaną
p – obiektywne prawdopodobieństwa trafienia kursu dziesiętnego k
Więcej o Value przeczytasz w artykule valuebet.
Tam gdzie występuje prawdopodobieństwo matematyczne, statystyczne lub szacunkowe, tam występuje ryzyko.
Działanie w warunkach ryzyka oznacza podejmowanie decyzji co do zdarzeń, które mogą wystąpić z określonym prawdopodobieństwem.
Często przy podejmowaniu decyzji można oszacować potencjalne zyski/straty, ale niemożliwe jest przypisanie im konkretnego prawdopodobieństwa. Mówimy wtedy o działanie w warunkach niepewności.
3. Parametry ryzyka w zakładach
Najwięcej zaobserwujemy zdarzeń w pobliżu wartości oczekiwanej, ShutterStock
3.1. Co oznacza ryzyko?
W życiu codziennym czy w zakładach często mówimy o małym, średnim czy dużym ryzyku. Ale jak to zmierzyć dokładnie? Jak sobie wyobrazić ryzyko?
Ryzyko wyobrażamy sobie często na zasadzie porównania.
Każdy zgodzi się chyba z tym, że postawienie na zakładu za 25 PLN jest bardziej ryzykowne od postawienia kwoty 1 PLN.
Podobnie zakład za 25 PLN z szansą wygranej 50% jest mniej ryzykowny niż zakład za 25 PLN z szansą trafienia 25%.
W końcu postawienie 25 PLN na raz jest bardziej ryzykowne niż postawienie 25 razy zakładu po 1 PLN.
Te przykłady z życia codziennego czy zakładów, znajdują odzwierciedlenie w wartościach pomiarowych ryzyka.
Wartość ryzyka w zakładach bukmacherskich mierzymy najczęściej za pomocą zestawu 3 parametrów:
- Kurs bukmacherski – stosunek wartości potencjalnego zysku do ryzykowanej kwoty. Im większy kurs, tym większe ryzyko. Im większa stawka tym większe ryzyko. Jeśli w danej sytuacji nic nie możemy stracić, a możemy tylko zyskać, to w bukmacherce mówimy, że mamy greenbook.
- Prawdopodobieństwo uzyskania zysku.
- Odchylenie standardowe, które wylicza się z wartości punktów 1 i 2. Im większe odchylenie tym większe ryzyko.
3.2. Przykład pomiaru ryzyka
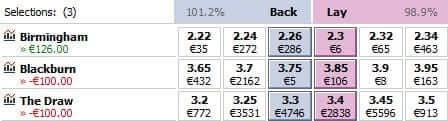
W powyższym przykładzie kurs wynosi 2,26. Gracz ryzykuje 100€ dla uzyskania 126€ (minus prowizja giełdy zakładów).
Prawdopodobieństwo sukcesu załóżmy, że wynosi dla uproszczenia 50%, a zatem wartość Value = 1/2⋅2,26=1,13 i jest większa od 1. Oznacza to dodatnią wartość oczekiwaną, czyli zakład teoretycznie opłaca się postawić.
Do policzenia wariancji W, dzięki której policzę odchylenie, mamy dane:
w1 = 126€,
w2 = -100€,
p1 = p2 = 50%.
Podstawiając do wzoru otrzymujemy:
W = p1⋅(w1-EV)^2+p2⋅(w2-EV)^2 = 1/2⋅(126€-13€)^2 +1/2⋅(-100€-13€)^2 = 6384,5 + 6384,5 = 12 769€
σ = sqrt(W) = 113€
Odchylenie standardowe sigma σ dla tego konkretnego zakładu wynosi 113€.
Dla porównania policzmy wariancję i odchylenie dla 2 razy mniejszej stawki z 2 razy większym kursem i taką samą wartością Value = 1,13. Mamy dane:
kurs k = 4,52
w1 = 176€ (bo (4,52-1)⋅50€=176€)
w2 = -50€
p1 = 25%, p2 = 75%,
Value = p ⋅ k = 1,13
z których otrzymujemy:
EV = 1/4⋅176€ + 3/4⋅(-50€) = 6,5€
W = 1/4⋅(176€-6,5€)^2 +3/4⋅(-50€-6,5€)^2 = 7182,56€ + 2394,19€ = 9576,75€
σ = 97,86€
Okazuje się, że grając 2x mniejszą stawką 2x większe kursy zmniejszamy podejmowane ryzyko.
Gra jest tym bardziej ryzykowna, im większy jest rozrzut jej wyników i im częściej pojawiają się wyniki najbardziej oddalone od wartości oczekiwanej gry.
3.3. Odchylenie standardowe
Odchylenie standardowe jest na tyle ważnym parametrem, że postanowiłem poświęcić mu więcej uwagi.
Pomaga odpowiedzieć na kluczowe pytanie: co jest bardziej ryzykowne?
3.4. Wyniki
Do policzenia wyników stworzyłem arkusz Excel i nazwałem go Risk Manager (skasował mi się niestety, ale nie jest potrzebny). Mogłem w nim edytować stawkę, kursy i wartość Value, w wyniku czego otrzymałem wartość odchylenia standardowego jako miarę ryzyka wraz z odpowiednim wykresem.
Tabele przedstawiają wartości odchylenia standardowego dla stawek 25, 50, 100, 200, 400 i 800 euro wpisanych w zielonych polach. Oczywiście wartości zostaną niezmienione przy zmianie waluty np. na PLN.
W szarych kolumnach są wartości odchylenia dla Value 0.9, 1.0, 1.1 i 1.2, które to Value są wyznacznikiem umiejętności gracza.
W niebieskiej kolumnie przyjąłem najbardziej reprezentatywne wartości kursów: 1.1 , 1.20, 1.33, 1.50, 1.80, 2.0, 2.25, 3.0, 4.0, 6.0, 11.0.
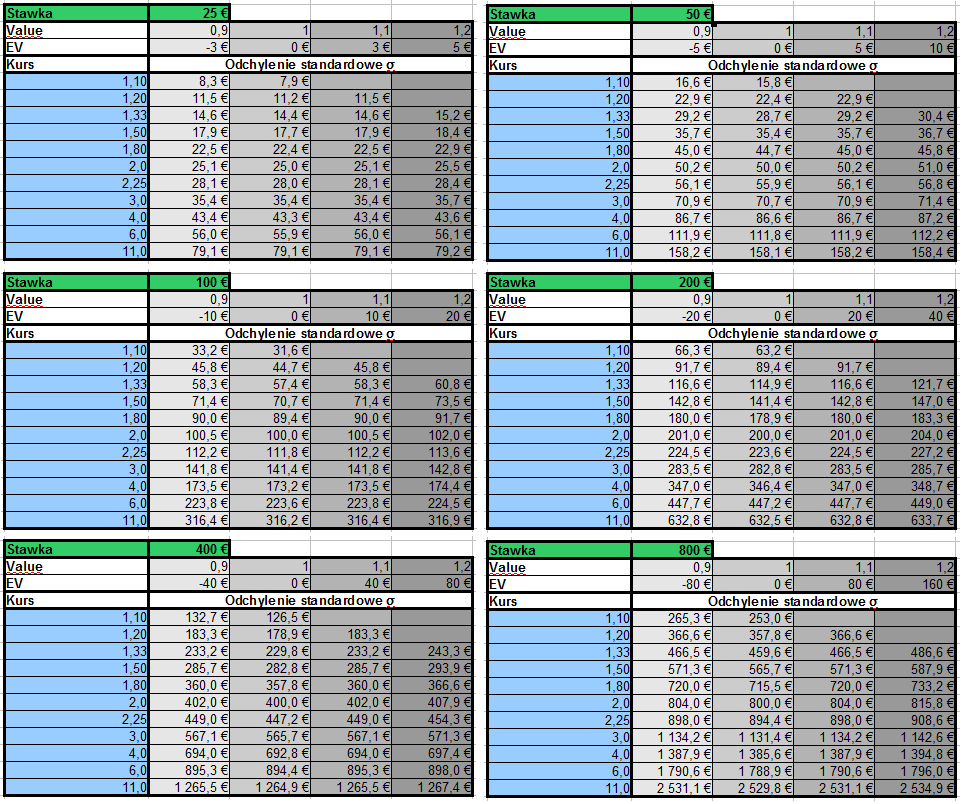
Wielkość ryzyka w zależności od stawki, value i kursu, SureBety.pl
Widać, że wraz ze wzrostem kursu, ryzyko nie rośnie liniowo, lecz logarytmicznie. Można nawet policzyć dosyć szybko zależność między kursem z przedziału 1.10 – 6.0 a odchyleniem standardowym korzystając ze wzoru krzywej regresji σ(k).
Ponadto jeśli przyjąć, że krzywa regresji ma postać σ(k) = a⋅ln(k)+b , gdzie a,b to parametry funkcji odchylenia standardowego dla kursu k z przedziału 1.10 – 6.0, to widać liniową zależność tych parametrów od wielkości stawki. Na wykresie można zaobserwować, że wzrost stawki razy 2 spowodował wzrost parametrów a, b razy 2.
Ta zależność jest prawdziwa dla każdej stawki z tego przedziału kursów, co wynika ze wzoru na odchylenie standardowe.
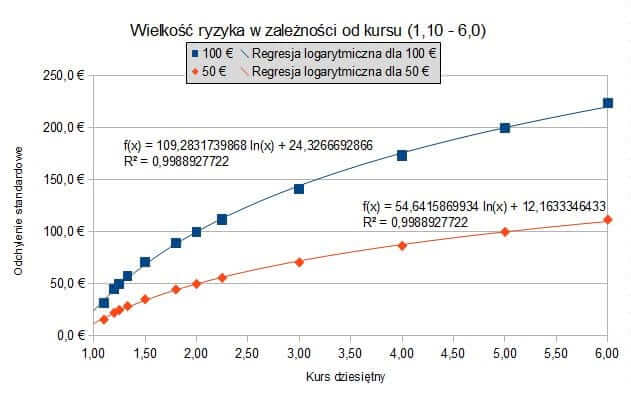
Wielkość ryzyka dla niskich kursów, SureBety.pl
Krzywa regresji zachowuje swój kształt także dla wyższych kursów. Na poniższym wykresie rozważyłem zakres kursów 2.0 – 101. Zmienił się jednak wzór krzywej regresji σ(k) z logarytmicznej na potęgową, gdyż ta druga daje lepsze dopasowanie R2 = 0,994 (dla logarytmicznej R2 ≅ 0,946).
W tym drugim wykresie stawka zmienia jedynie parametr a, zostawiając niezmieniony wykładnik potęgi.
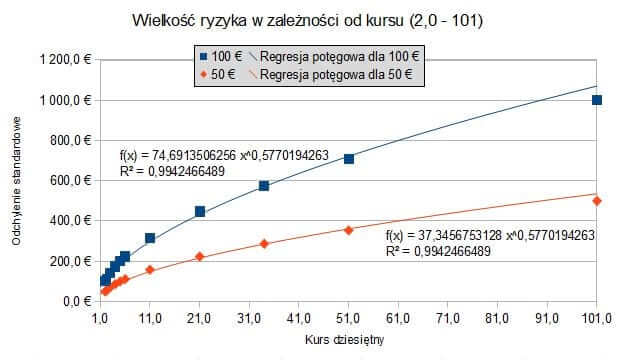
Wielkość ryzyka dla wysokich kursów, SureBety.pl
3.5. Wyprowadzenie wzorów
1. Wyprowadzenie równania 1.2:
EV = p1⋅w1+p2⋅w2 /:s
EV/s = p1⋅ w1/s – p2⋅s
Podstawmy p1=p i p2=1-p i uwzględnijmy, że kurs k = w1/s + 1 ⇒ w1 = s⋅(k-1), gdzie s – stawka, w2=-s:
EV/s = p⋅(k-1)-(1-p) = p⋅k-p-1+p = p⋅k – 1 = Value – 1
EV = (Value – 1)⋅s
cnd.
2. Można też wyprowadzić wzór na wiariancję W, która spierwiastkowana daje odchylenie standardowe σ:
W = p1(w1-EV)^2+p2(w2-EV)^2
Korzystając z tego że w1 = s⋅(k-1) i w2 = -s:
W = p⋅( s⋅(k-1)-EV )^2 + (1-p)⋅(-s-EV)^2
Wprowadzając kosmetyczne zmiany otrzymujemy ostatecznie:
W = p⋅( (k-1)⋅s – EV )^2 + (1-p)⋅(s+EV)^2 (równanie 1.3)
σ = √(W)
3. W wyniku obliczeń otrzymałem dwa wzory estymujące wartość ryzyka w zależności od kursu:
σ1 (k) = 109,283 ⋅ ln(k) + 24,327 dla stawki 100€ i kursów z zakresu 1,10 – 6,0
σ2 (k) = 74,691 ⋅ k0,577 dla stawki 100€ i kursów z zakresu 2,0 – 101,0
σ3 (k) = 88,143100 ⋅ k0,529224 dla stawki 100€ i kursów z zakresu 6,0 – 101,0 z R2 = 0,9995
Można zatem przyjąć wzór na obliczanie odchylenia standardowego w zależności od kursu i stawki:
σ (k, s) = 1,09283⋅s ⋅ ln(k) + 0,24327⋅s dla k∈[1.10;6]; 0,88143100⋅s ⋅ k0,529224 dla k∈(6, 101] (równanie 1.4)
Dla wartości granicznej k=6,0 otrzymujemy odpowiednio 220,1€ z pierwszej części wzoru lub 227,5€ z drugiej części wzoru.
Pierwsza wartość jest bliższa prawidłowej wartości 223,6€.
4. Można się także pokusić o przybliżone równanie kursu w zależności od zadanej wartości σ i stawki s.
Pierwszą część równości można odwrócić tak:
σ (k, s) = a⋅s ⋅ ln(k) + b⋅s
k (σ, s) = e^[(σ-bs) / as] dla 1,10
Drugą część równości można odwrócić tak:
σ (k, s) = a⋅s ⋅ kb
k (σ, s) = (σ/as)^(1/b) dla as⋅6^b<σ⋅b ⇔ 2,275⋅s<σ<10,137⋅s
Otrzymujemy zatem przybliżone równanie kursu w zależności od zadanej wartości σ i stawki s:
k (σ, s) = exp[(σ-0,24327⋅s)/(1,09283⋅s)] dla σ∈[0,347444⋅s ; 2,201663⋅s]; ( σ/(0,881431⋅s) )(1/0,529224) dla σ∈(2,275⋅s ; 10,137⋅s] (równanie 1.5)
Analogicznie można by wyprowadzić wzór na s(σ,k). Choć przy obecnej technologii pewnie lepiej skorzystać z Excela lub z liniowej zależności stawki od odchylenia standardowego.
3.6. Wnioski
Jakie wnioski płyną z tych obliczeń i wykresów?
- Odchylenie standardowe prawie nie zależy od wartości Value.
- Wartość odchylenia standardowego wzrasta liniowo ze wzrostem stawki.
- Wartość odchylenia standardowego wzrasta logarytmicznie lub potęgowo wraz ze wzrostem kursu.
- Stawianie zakładu za 100€ po kursie 2.0 jest tak samo ryzykowne (σ=100€) jak stawianie 200€ po kursie 1,25 czy 50€ po kursie 5.0.
- Gracz, który postanowił łączyć kursy 2.0 w kupony AKO, powinien zmniejszyć ok. 2-krotnie stawkę na kupon za każde dodatkowe zdarzenie z kursem ok. 2.0 dodane do kuponu. Przykładowo jeśli grał single z kursem 2.0 po stawce 100€, na duble z kursem 4.0 powinien stawiać 58€, na treble z kursem 8.0 powinien postawić 38€ aby zachować ten sam poziom odchylenia σ=100€. Osobiście uważam, że stawki odpowiednio: 100€ – 50€ – 25€ też będą dobre i lepiej zadbają o płynność finansową. Podobne rozumowanie można przeprowadzić dla innej wartości kursów.
- Można z dużą dokładnością wyznaczyć wartość odchylenia standardowego z równania 1.4 przy danym kursie i stawce lub stawkę czy kurs za pomocą pozostałych dwóch zmiennych (przykład wyprowadzenia powyżej). Ewentualnie skorzystać z arkusza excel, który szybko policzy tą wartość dokładnie.
- Podane obliczenia można łatwo wykorzystać do porównania systemów stawkowania między sobą.
Jak widać możliwości wykorzystania tej wiedzy jest wiele.
4. Metody ograniczania ryzyka
4.1. Minimalizuj ryzyko bankructwa
Głównym celem zarządzania jest ograniczanie ryzyka bankructwa, czyli przetrwanie. Drugi cel to wypracowanie stałych profitów, a trzeci to wysokie zyski. Chyba nie muszę tłumaczyć dlaczego taka kolejność? Bez pierwszego punktu pozostałe jednak nie mają znaczenia.
4.2. Kto pierwszy zbankrutuje?

Bogaci mają więcej możliwości, ShutterStock
Wyobraź sobie, że Ty i ja stawiamy 1 PLN na rzut monetą: orzeł – wygrywasz, reszka – przegrywasz. Załóżmy, że masz do dyspozycji 1000 PLN, a ja 100 PLN. Mimo że dysponuję mniejszą kwotą, możemy grać długo – musiałbym ponieść 100 strat więcej niż wygranych, aby zbankrutować. Możemy tak grać długo, chyba że dołączy do nas pośrednik i zacznie pobierać opłaty.
Nasze szanse bankructwa zmienią się jednak diametralnie jeśli podniesiemy zakład do 25 PLN. Wtedy seria, w której jest zaledwie o 4 orły więcej, kończy dla mnie grę. Ty zaś możesz sobie pozwolić na serię z 39 reszkami więcej. Gdy pozostałe czynniki są stałe dla obu graczy, pewnie biedniejszy gracz zbankrutuje, bo z prawdopodobieństwem 89% seria z 4 orłami przewagi zdarzy się wcześniej niż z 40 reszkami przewagi.
Większość graczy uważa się za bardziej inteligentnych od innych graczy i nie uważa, że pozostałe czynniki są stałe. Wtedy bukmacherzy spokojnie zarabiają na prowizji kosztem takich graczy. Biorąc jeszcze pod uwagę, że mają znacznie więcej kapitału do dyspozycji od każdego pojedynczego gracza, trzeba racjonalnie gospodarować swoimi środkami pieniężnymi.
4.3. Ryzykowne straty
Nie wystawiaj na ryzyko zbyt dużej części twojego kapitału. W czasie złej passy raczej zmniejszaj stawki niż zwiększaj. Większość graczy bankrutuje podczas próby “wyjścia z dołka”. Dobry system zarządzania trzyma Cię przede wszystkim z dala od dna.
Im głębiej wpadasz, tym bardziej śliski staje się “dołek”.
Jeśli stracisz 10%, musisz odrobić 11%, aby zrekompensować stratę. Jeśli stracisz 20%, to musisz odrobić już 25%. Tracąc 40%, potrzebujesz 67% zysku, a przy 50% stracie musisz zarobić 100% tylko po to by wyjść z powrotem na 0.
Wiedz na jakie straty możesz sobie pozwolić i kiedy powinieneś ciąć straty (np. zmniejszając stawkę na zakład lub zakończyć na danym stopniu progresji). Doświadczeni gracze przeczekują niebezpieczeństwo wracając na rynek zakładów w odpowiednim momencie po ochłonięciu z emocji. Dodatkowo ograniczają ryzyko. Amatorzy działają nadal pod wpływem emocji, chcąc się odegrać. Nie zmieniają wysokości podejmowanego ryzyka licząc na szczęście.
Dywersyfikacja jest jedną z najprostszych metod ograniczania ryzyka, ShutterStock
4.4. Dywersyfikacja ryzyka
Dywersyfikacja ryzyka to nic innego jak rozdzielanie ryzyka na (bardzo) wiele stawek. Proces ten zmniejsza podejmowane ryzyko. Co prawda przy 10 zakładach po 1 PLN, potencjalna strata będzie taka sama jak przy 1 zakładzie za 10 PLN, ale dywersyfikując w ten sposób ryzyko na kilka zakładów, nasza strata będzie z przedziału 0-10 PLN, zaś w drugim przypadku albo 0 albo 10 PLN. Przypadek zdywersyfikowany jest więc mniej ryzykowny (kurs i wartość oczekiwana te same, ale mniejsze odchylenie standardowe).
Podobnie mniejsze odchylenie standardowe będzie w przypadku zagrania 10 kuponów po kursie @2.0 niż 1 kuponu po kursie @20.
5. Szczególne przypadki ryzyka
Gracz musi uwzględnić także niestandardowe przypadki, które mogą zmniejszyć dostępny kapitał.
- Ryzyko utraty połączenia z Internetem. Do tego przypadku zalicza się także awaria komputera/laptopa/prądu. Zostaje wtedy możliwość skorzystania z telefonicznego kanału kontaktu z bukmacherem/giełdą lub znalezienie innego stanowiska z dostępem do Internetu. W przypadku obstawiania zakładów na żywo za duże kwoty, posiadanie dwóch niezależnych źródeł dostępu do Internetu ogranicza wpływ tego ryzyka.
- Ryzyko problemów technicznych po stronie bukmachera/giełdy. Gracz nie może wtedy żądać odszkodowania za straty. Można zmniejszyć wpływ tego ryzyka poprzez kontakt telefoniczny z giełdą (anulowanie otwartych pozycji) lub ulokowanie środków finansowych u bukmacherów i w portfelach internetowych tak, by można było szybko skontrować otwartą pozycję. Alternatywnego bukmachera ze środkami na koncie zawsze warto mieć otwartego.
- Ryzyko za małej płynności na rynku. Może się okazać, że na giełdzie zakładów zabraknie chętnych, by móc zamknąć pozycję, zwłaszcza na rynku na żywo.
- Ryzyko błędu wyniku na żywo. Wyniki podawane u bukmacherów są tylko informacyjne, a bukmacherzy nie odpowiadają za podawane informacje. Do obowiązku gracza należy znalezienie transmisji z minimalnym opóźnieniem obrazu/wyniku.
- Ryzyko wysłania błędnego zlecenia. Szczególnie w rynkach na żywo, w wyniku pośpiechu lub przeoczenia może wystąpić któryś z błędów: źle wybrany rynek, źle wpisany/wybrany kurs czy źle wpisana stawka. Większość systemów wymaga potwierdzenia przyjęcia zakładu. Szybki “rzut okiem” przed przyjęciem zakładu jest zawsze konieczny. W programach tradingowych, wyświetlenie trybu drabinkowego (na jedno kliknięcie) pozwala przyspieszyć transakcje minimalizując ryzyko błędnego zlecenia.
- Ryzyko nie przyjęcia zakładu lub zmiany kursu. Gracz z czasem powinien zauważyć zależności kiedy jaki bukmacher/giełda zmieniają kursy i jak bardzo mogą się one zmienić. Przed nagłym zamknięciem rynku (np. z powodu gola) mogą częściowo ochronić szybkie transmisje. W minimalizowaniu czasu stawiania zakładu (kontrującego), na giełdzie zakładów, pomagają programy do tradingu, które uważam za obowiązkowe dla graczy z poważnym podejściem do tradingu.
- Ryzyko różnic w regulaminach bukmacherów. Przy obstawianiu przeciwnych zdarzeń u bukmacherów, może się okazać, że sposób rozliczenia zdarzenia różni się. Klasycznym przykładem jest rozliczanie kreczy w tenisie ziemnym. Trzeba znać regulaminy bukmacherów z dyscyplin, które się obstawia. Różnice najlepiej sobie spisać.
- Ryzyko ustawienia meczu. Może się okazać, że mecz nie będzie “czystą” rywalizacją. Podejrzanie wysoki kurs na jednego z zawodników powinien być dla gracza sygnałem alarmowym, że coś jest nie tak.
6. FAQ – pytania dotyczące ryzyka w zakładach
6.1. Którą linię under/over z value warto obstawiać?
Jeśli zauważyłeś, że potrafisz lepiej oszacować w piłce nożnej główną linię under/over 2,5, to może się okazać że bardziej ci się opłaca grać inne linie. Pozostałe linie są zawsze odpowiednich proporcjach zależne od linii głównej a zatem jeżeli na głównej linii występuje błąd to na liniach zależnych także będzie występował błąd. Bardzo możliwe że będzie nawet większy niż na linii głównej.
Załóżmy, że na linii głównej przy kursach około @2.0 potrafisz regularnie znaleźć value=1,10. To oznacza, że na under 1,5 oraz over 3,5 pewnie będzie value 1,15-1,20, a dla under 0,5 oraz over 4,5 value może być jeszcze większe. Kursy natomiast też będą znacząco większe i spowodują większe wahania kapitału, jeśli stawki pozostaną bez zmian.
Zacząłbym od policzenia wartości Value dla głównej linii under/over 2,5.
Potem to samo należy zrobić dla linii sąsiednich, czyli under/over 1,5 oraz under/over 3,5.
Kurs będzie wyższy niż na głównej linii dla undera 1,5 i dla overa 3,5.
Obstawianie ich taką samą stawką będzie powodowało wyższe wahania kapitału.
Będzie to uzasadnione tylko w przypadku, gdy value jest odpowiednio większe niż dla głównej linii, na przykład value=1,20 zamiast 1,10.
Dokładne wartości zależą od konkretnego przypadku i trzeba by je policzyć. Nie jest to łatwe.
Modele matematyczne powinny być dla Ciebie dobra inspiracją do dalszych badań.
Zamiast obliczać teoretyczną wartość można po prostu posłużyć się historycznymi danymi, jeśli masz taką możliwość.
Wystarczy zebrać dużo danych i przeanalizować jak wielkość stawek i kursów wpłynie na wielkość wahania kapitału.
Pamiętaj, że nie liczy się tylko zysk, ale także to, aby wahania nie były zbyt duże.
Przy większych kursach powinno się zmniejszyć stawkę, aby zachować ten sam poziom ryzyka.
Literatura
[1] Teresa Kamińska – Teoria ryzyka [PDF 214 kB]Polecany bukmacher:

Przepraszamy.
Jak możemy poprawić artykuł?
Dziękujemy za przesłanie opinii.




